最近在改善 DN11 的网络拓扑前端展示效果,在图结构上做了不小的调整,记录一下。
边中心度
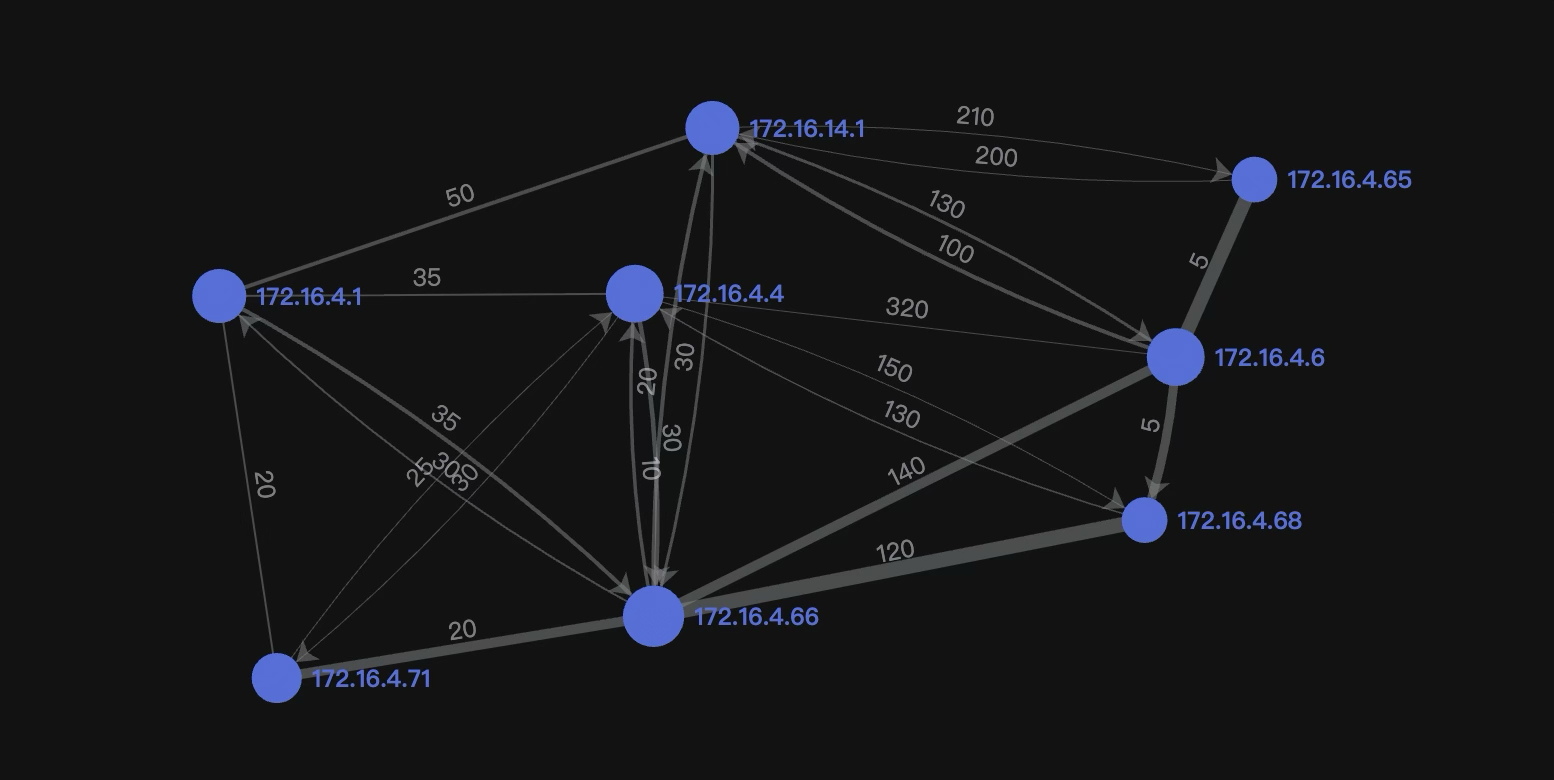
上面展示的是我的 OSPF 网络拓扑,可以在 https://status.dn11.top/#/ospf/4220084444 看到实时的图像。
除了你见过的所有的 OSPF 拓扑图都会展示的 cost 和 routerId 一类的基本结构,你会很容易地注意到:这里的每一个边都有宽度。这就是边中心度在图中的展示方式。
边中心度这个概念简单来说就是通过某条边的最短路径的数量再做一点归一化,归一化前的边 $e$ 的中心度可以用这个公式表示:
$$ c(e) = \sum_{s, t \in V} \frac{\sigma(s, t | e)}{\sigma(s, t)} $$
摘自 networkX
需要注意的是不同于 networkX 的表述,本文的“边”均为有向边
$V$ 所有节点的集合,$\sigma(s, t)$ 是 $(s 到 t)$ 间最短路径的数量,$\sigma(s, t | e)$ 是其中经过有向边 $e$ 的最短路径的数量。
具体的公式相比前面的描述而言将 ECMP 路由纳入了考虑,将权重分给了 ECMP 路由。
归一化
为了在节点数量变化的情况下持续评估边中心度,我给边中心度做了一次归一化,简单来说就是除以当前节点数量 $n$ 下可以达到的边中心度的最大值。
$$ c_{max}(n) = \begin{cases} 0& n<2 \ (n-1)(n-2)+1 &n>=2 \end{cases} $$
下面给出最大值的证明:
$n = 1$ 时,显然 $c_{max} =0$;
$n = 2$ 时,显然 $c_{max} =1$ 满足 $(n-1)(n-2)+1$;
$n >= 3$ 时,取边中心度最大的有向边 $ab$,方向从 $a$ 到 $b$
对于节点 $b$,从 $b$ 出发最短路径不可能经过有向边 $ab$,共计 $n-1$ 条
对于节点 $a$,以 $a$ 为终点的节点不可能经过有向边 $ab$,共计 $n-1$ 条
其中以 $b$ 为起点 $a$ 为终点的边被重复统计
可以得到
$$ c_{max}(n) <= (n-1)(n-2)+1 $$
下面证明等于号可达性
构造步骤:
- 取任意两个节点,作有向边 $ab$, 令 $cost=1$
- 取剩余所有节点 $c_n$,作有向边 $bc_n$, $c_na$, 令 $cost=1$
此时所有 $c_n$ 节点到除 $a$ 节点和自身外的节点的最短路径都要经过边 $ab$,得到 $(n-2)^2$
$a$ 节点到所有节点都需要经过边 $ab$,得到 $n-1$
总计 $(n-1)(n-2)+1$ 条边,原式得证
最后,归一化的式子总结为:
$$ c_{normalized}(e) = \frac{\sum_{s, t \in V} \frac{\sigma(s, t | e)}{\sigma(s, t)}}{c_{max}(n)} $$
实现
实现节点中心度计算的时候给专门抽象了一个用于图结构分析的数据结构,现在又派上用场了,在这里新增加了一些计算函数。
计算所有边中心度的复杂度相当于一次全源最短路,还是比较费 CPU 的操作,因此设计上把全边中心度的计算放在了后端,每次拓扑图刷新的时候会跟着一起重新计算一次。此外还由于和中介中心度一样都依赖全源最短路,还做了一点缓存,防止重复计算。
对于 DN11 的 BGP,由于没有上下游的概念,就直接抽象成 cost 为 1 的双向有向图进行计算了。
最终将这些数值在前端再映射到边的宽度上,就是现在你能看到的图了。
这一改动在不增加交互负担的前提下,带来了一些好处:
- 直观地看到哪些边是网络的主干
- 直观地看到哪些边极少或者从未有路由经过
- 大多数情况下可以直接看出任意两点之间到最短路
最短路径树(图)
很多 OSPF 拓扑图实现都提供了绘制某两个节点之间的最短路径的能力。这确实是一个比较实用的功能,尤其是在较大的网络中。
不过 NetworkMonitor 会采用另一种绘制方法 —— 最短路径树(图)。考虑 ECMP 时它是一个有向无环图,不考虑 ECMP 时比较干脆就是一个树。
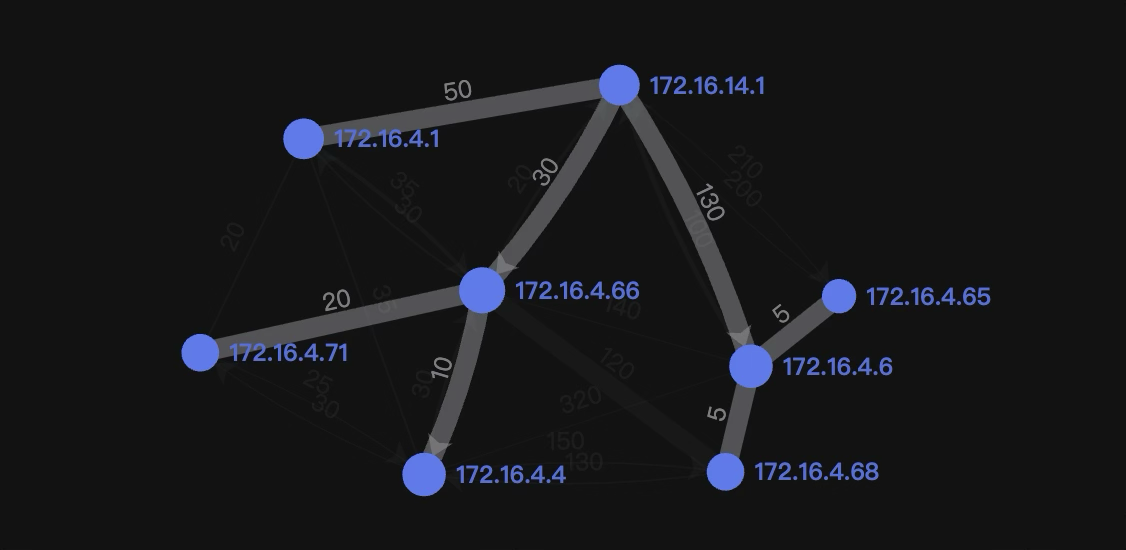
图中展示了从 172.16.14.1 出发的最短路径树,这几乎就是我心目中展示 OSPF 路由最清晰的方式了。
树证明
下面证明不考虑 ECMP (从根到任意节点有且只有一条最短路) 时,从一个节点出发到其他所有节点的最短路径组成的有向图是有向树:
只需证明除根以外的所有的节点入度均为 1
假设存在一个非根节点 $a$ 的入度为 0,那么从根到节点 $a$ 不存在路径,与条件冲突,所以不存在入度为 0 到非根节点
假设存在一个非根节点 $a$ 的入度大于 1,那么从根出发过节点 $a$ 至少存在 2 条最短路径 $P_1,P_2$ 分别途径对应 $a$ 入度的有向边 $e_1,e_2$
在节点 $a$ 截断 $P_1,P_2$,取从根出发到节点 $a$ 路径为 $P_{ra1},P_{ra2}$
由于最短路的子路径也是最短路,$P_{ra1},P_{ra2}$ 都是从根到节点 $a$ 的最短路,与条件冲突,所以不存在入度大于 1 的非根节点
综上,所有非根节点的入度均为 1
原命题得证
实现
由于只给 OSPF 配了最短路径树功能,外加上点击后才会需要这部分数据,最短路径树的计算被放在了 NetworkMonitor 的前端。
实现采用了一种基于 dijkstra 思想的算法,一次遍历获取到最短路径树,俺寻思的产物,下面简要介绍一下:
function getEdgeIndexesInShortestPathOf(src: string) {
let node_distance:Map<string, number> = new Map();
node_distance.set(src, 0);
let unvisited_links: Array<LinkWithIndex> =
all_links.map((e, i) => {
return {
index: i,
link: e,
}
}) || []
let visited_links: Array<LinkWithIndex> = []
let found_new_node_pos = 1;
while (node_distance.size <= nodes.length && unvisited_links.length > 0) {
let allow_start = Array.from(node_distance.keys());
let min_cost_edge = unvisited_links.filter((e) => allow_start.includes(e.link.src)).reduce<LinkWithIndex | null>((min_cost_edge, e) => {
if (min_cost_edge === null) return e;
if (e.link.cost+node_distance.get(e.link.src)! < min_cost_edge.link.cost+node_distance.get(min_cost_edge.link.src)!) return e;
return min_cost_edge;
}, null)
if (min_cost_edge === null) break;
unvisited_links = unvisited_links.filter((e) => e.index !== min_cost_edge.index);
if (node_distance.get(min_cost_edge.link.dst) === undefined || node_distance.get(min_cost_edge.link.dst)! === node_distance.get(min_cost_edge.link.src)! + min_cost_edge.link.cost) {
node_distance.set(min_cost_edge.link.dst, node_distance.get(min_cost_edge.link.src)! + min_cost_edge.link.cost);
visited_links.push(min_cost_edge);
found_new_node_pos = visited_links.length;
}
}
return visited_links.slice(0, found_new_node_pos)
}
- 初始化空 Map
node_distance用于记录从根到所有节点的最短距离,设置从根到根的距离为0。 - 初始化集合
unvisited_links,visited_links,将所有的边放入unvisited_links - 初始化变量
found_new_node_pos为1,用于最终截断 - 循环直到所有节点的都被计算了出来或不存在未访问过的边
- 从
node_distance的key中提取已访问过的节点,过滤出这些节点的所有未访问出度边 - 对于上述所有的出度边
a计算node_distance[a.src]+a.len,取结果最小的边,移出unvisited_links集合 - 若
node_distance[a.dst]为null,记录node_distance[a.dst]=node_distance[a.src]+a.len - 若
node_distance[a.dst]=node_distance[a.src]+a.len将这条边加入visited_links集合并更新 found_new_node_pos 为当前visited_links长度
- 从
- 返回
visited_links[:found_new_node_pos]左闭右开
简单来说就是从 dijkstra 拓展出多个最短路 + 满足一定条件时的记录边
后记 1 —— Story
NetworkMonitor 此前一直都没有加入最短路计算的能力,一方面是我觉得点选两个点这样算一下是一件比较麻烦的事情,另一方面,就 DN11 现在的规模而言,很难说的上是需要这样的一个功能。BGP 图本来就是不精确的,寻路只会产生误导,OSPF 图展示的大多是个人网络,只有少数人的网络规模达到了一眼看不穿最短路的状态,所以我判断这个功能加了也不会有什么人在用的。
另外我一直也没想到一个比较满意的交互方式,自从做了点击查看节点 uptime 后我对这类东西是谨慎又谨慎,uptime 那个实在是太难用了。这个难用是多方面原因造成的,一方面是后端这边没有太多精力去搞 SQL 优化,准确说是 Flux 优化,导致查询非常慢,主要是几个 group 导致的,另一方面前端误触尤其是移动端,比较严重,动画也比较拖沓,总之体验很差。
这次直接把 uptime 这块删掉了,把点击交互的结果置换成了显示最短路径图。这样即时性比较强,也不会突脸一个弹窗打断注视图像的目光。已经是相当友好的选择了。
在注意到最短路径组成的图极有可能是树前,我其实对最短路径图是不屑一顾的。图里弯弯绕绕的隐去了几个无关边而已,一些量变罢了,稍微好看一点。前段时间撸串的时候 Potat0 来和我推销这个最短路径图,这会才突然注意到,这可能是一个树,即使带上 ECMP 也起码是一个 DAG。这就完全不一样了,这次是真的有质变。不过年前没什么空,现在似乎所有人所有公司都在忙着搞 AI,我也成不了例外,年后才把这个新特性端出来。
后记 2 —— Inventor
我似乎挺乐于"重新发明"一个东西。
不过对我而言这不是“重新发明”,而是“发明”,只不过已经被前人发明过了,我不知道而已,某种意义上也算是共同发明了,至少我是这么想的。
我不知道路径中心度和最短路径树这些概念是否已经在世界的另一个角落被用于展示网络拓扑了,我没找到。但,无论如何,此刻我更享受的是创造的满足感。
发明
提到“发明”你可能脑子里浮现的是爱迪生发明电灯、张衡发明地动仪,还有我们的祖师爷,冯·诺伊曼和图灵发明计算机那样的事情。他们都是响当当的大人物,和我们?侥幸活在新时代的小人物相提并论简直是 —— 大逆不道有点过了,至少是难以想象。“发明”这个词一直以来都给人一种比较严肃的感觉,仿佛一定要做出什么新的、有用的东西来一样。
我要对这个概念提出挑战。Minecraft 的赤石科技是发明,机械动力玩家的俺寻思之力也是发明,我这篇文章记录的算法也是发明,就是普遍意义上的发明。
诚然,这些小玩意远远不如那些为大众所熟知的发明来的震撼,我也无意强迫所有人承认这些小玩意是与它们等价的事物,但不容置喙的是所有发明人的心都是一样的。我们会倾注自己的心血在探索未知的事物,尝试组合规律并构造一个可以工作的结构,没有人会怀疑这所有的过程中的赤诚之心。基于此,所有享受这一过程的人和那些响当当的大发明家都是完全平等的。
重新发明
重新发明是一件很浪漫的事情。跨越千年的两个灵魂,虽然完全不知道彼此是谁,但可以知晓的是,那一刻两个灵魂在这件事情上产生了共振,多么不可思议。
重新发明的门槛并不高,在杭电读书的时候听闻老师讲了浙大计算机的一些课程安排,老师们正在往这个方向努力。这个课程安排先教数电,做一些亮闪闪的小灯,再用同一块板子同一套技术栈在计算机组成原理的课上实现一个自己的 CPU ,随后实现一个自己的操作系统并运行在自己的 CPU 上。这完全可以说的上是重新发明了计算机。相信未来的科班学生毕业前都能够重新发明一次计算机(真的假的?)。
DN11 也是一种重新发明 —— 重新发明互联网。我们会从拉网线(其实是隧道)开始,逐步配置路由协议,允许 DNS 和 HTTP 运行;从 Web1.0 时代出发,一步一坑地往现代互联网前进。(虽然 DN11 成立本意可能并不在此,但也不冲突)
重新发明也可以是一些更渺小一些的事物,这些东西就更容易做到从 0 重新发明了,除了本文的一些构思,SYN 扫描其实我也算是独立发明人。我写出我的 proxyScan 扫描器前其实并不知道这个世界上已经有了 SYN 扫描的概念了,虽然事后发现这个问题有点打击吧。虽然…,但总还是缺点什么。想着这个世界上的东西是不是快被发明完了,就像现在已经没有大航海时代的冒险家一样。不过其实能独立发明也证实了我其实起码有和当年搞 SYN 扫描的人一样的能力,只是可能世界还欠我一个证明,只能这样聊以自慰。
我已经什么都不缺了
或许,这个证明已经来了。
我是个相当在意别人看法的人,很多东西也就是心里想想,我今天写这篇后记不怕被人蛐蛐,是因为这个证明真的来了。它不是一个颠覆性的东西,但它真的有效且从未被人提过。
在这里预告一篇文章 —— 不是不到,只是时机未到。